최소제곱해(Least-Squares)와 정규방정식(Normal Equation)을 정리한다.
선형대수 수업에서 공부했던 내용이지만 많이 까먹어서 다시 공부해서 정리해 본다.
우선 The Best Approximation Theorem 이란 것이 있다.

우리는 어떠한 벡터를 찾고자 할 때, 낮은 차원에서 찾고자 하는 벡터와 가장 가까운 벡터를 찾는 것에 관심이 있다. 위와 같은 정리를 통해서 실수 공간에서 벡터와 해당 차원보다 낮은 차원에서 가장 가까운 벡터를 찾기 위해서는 Orthogonal Projection(정사영)을 이용하면 된다는 것이다.
<Least-Squares>
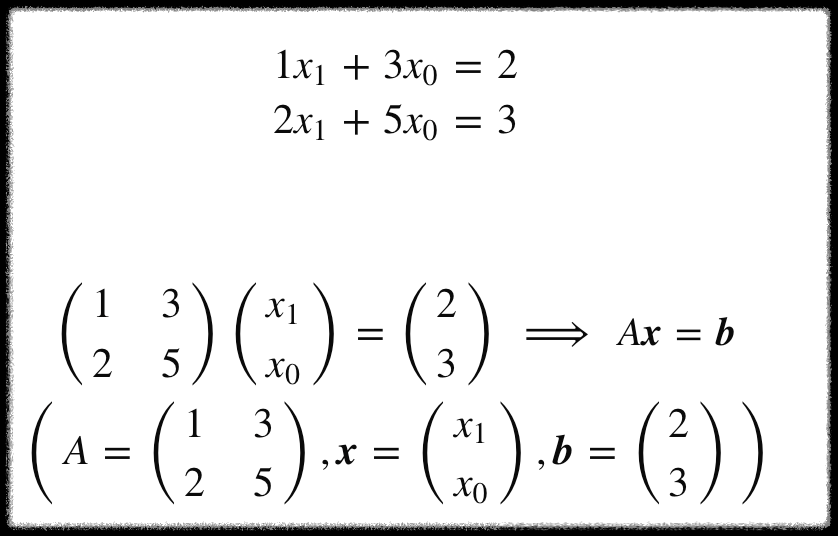
위는 주어진 식을 행렬로 표현한 것이다.
Ax는 A의 Column Space에 속하는 것이 확실하다. 그러나 b가 그렇다는 보장은 없다. 만약에 b가 A의 열공간에 속하는 경우 해를 찾을 수 있지만 그렇지 않은 경우는 해를 찾을 수 없다. 이러한 경우 차선책으로 해에 가장 근사하는 해를 구하는 것이다. 즉 Ax가 b와 최대한 가깝게 되는 x를 구하는 것이다.
b가 A의 열공간에 존재하지 않을때, A의 열공간에서 b와 가장 가까운점을 찾으면 된다. 위에서 언급한 The Best Approximation Theorem과 일맥상통 한다. A의 열공간에 존재하면서 b와 가장 가까운 것을 b`라고 한다면, b` 는 A의 열공간에 대한 b의 정사영(orthogonal projection onto column space of A)이다.
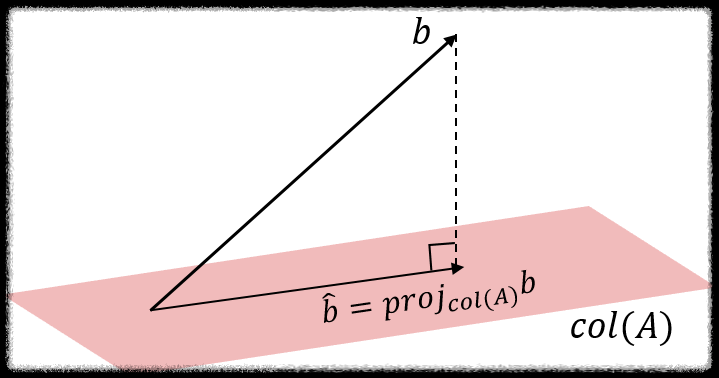
b` 는 A의 열공 간 안에 존재하므로, 식 Ax=b`는 이제 풀 수 있다. 이때의 해 x̂ 이 Ax=b의 최소제곱해 가 된다.
출처: https://soohee410.github.io/least_squares_sol
[선형대수] Least-Squares Solution, Normal Equation
[선형대수] Least-Squares Solution, Normal Equation Published Jan 27, 2020 <!-- --> 안녕하세요! 이번 포스트에서는 최소제곱해(Least Squares Solution) 과 정규방정식(Normal Equation) 에 대해 선형대수 과목에서 제가 배
soohee410.github.io
예제 및 참고하기 좋은 글이 있다.
http://matrix.skku.ac.kr/math4ai-intro/W5/
정사영과 최소제곱문제
matrix.skku.ac.kr
쉽게 생각해 보면 해가 존재하지 않는 방정식에 대해서 선형 연립 방정식을 세우고 행렬표현을 한다.

우리가 찾고자 하는 최소제곱하는 다음과 같다.

A = matrix([[1, 0], [1, 1], [1, 2], [1, 3]])
y = vector([1, 3, 4, 4])
print("u* =", (A.transpose()*A).inverse()*A.transpose()*y)파이썬 코드로는 위와 같다. 위의 공식을 통해서 최소제곱해를 구할 수 있다.
u* = (3/2, 1)위의 최소제곱해를 바탕으로 최소제곱직선을 그래프에 그리면 아래와 같다.
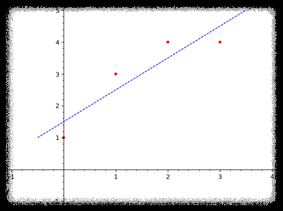
데이터의 분포와 유사한 선이 그어진 것을 볼 수 있다. 이러한 과정을 선형회귀(linear regression)이라고 한다.
<Normal Equation>
위에서 최소제곱해를 구하는 방법을 알아봤다. 행렬에 매번 정사영을 구해서 최소제곱해를 구하는 과정은 조금 비효율적일 수 있다.
따라서 대표적인 방법 중 하나인 정규방정식을 이용해 볼 수 있다. 정규 방정식은 특정 선형 회귀 문제에서 파라미의 최적값을 구하는 더 나은 방법이다.
어떤 비용 함수(Cost Function)가 존재할 때 parameter가 실수이자 스칼라라고 하자. 즉 벡터가 아니라 숫자인 경우 함수의 최솟값을 찾기 위해서는 미분해서 0이 되는 지점을 찾으면 된다.
문제는 파라미터가 실수가 아니라 n차원의 벡터일 때다. 모든 파라미터에 대해서 각각 편미분을 해주면 모든 파라미터의 최적값을 구할 수 있고 비용함수의 최솟값도 찾을 수 있다. 그러나 이 방법도 비효율적이다.
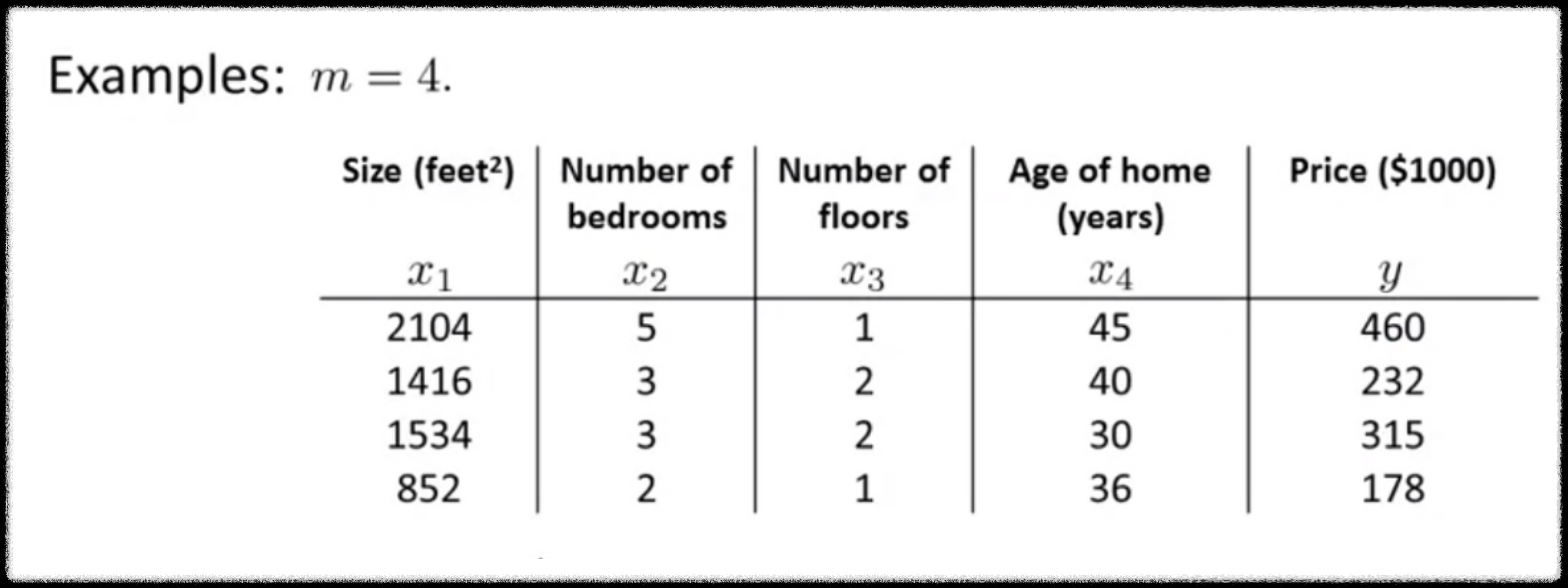
회귀문제에 어김없이 등장하는 부동산 price 문제다. feature의 개수가 4이고 데이터의 개수가 4인, m=4인 학습데이터 셋이 있다.
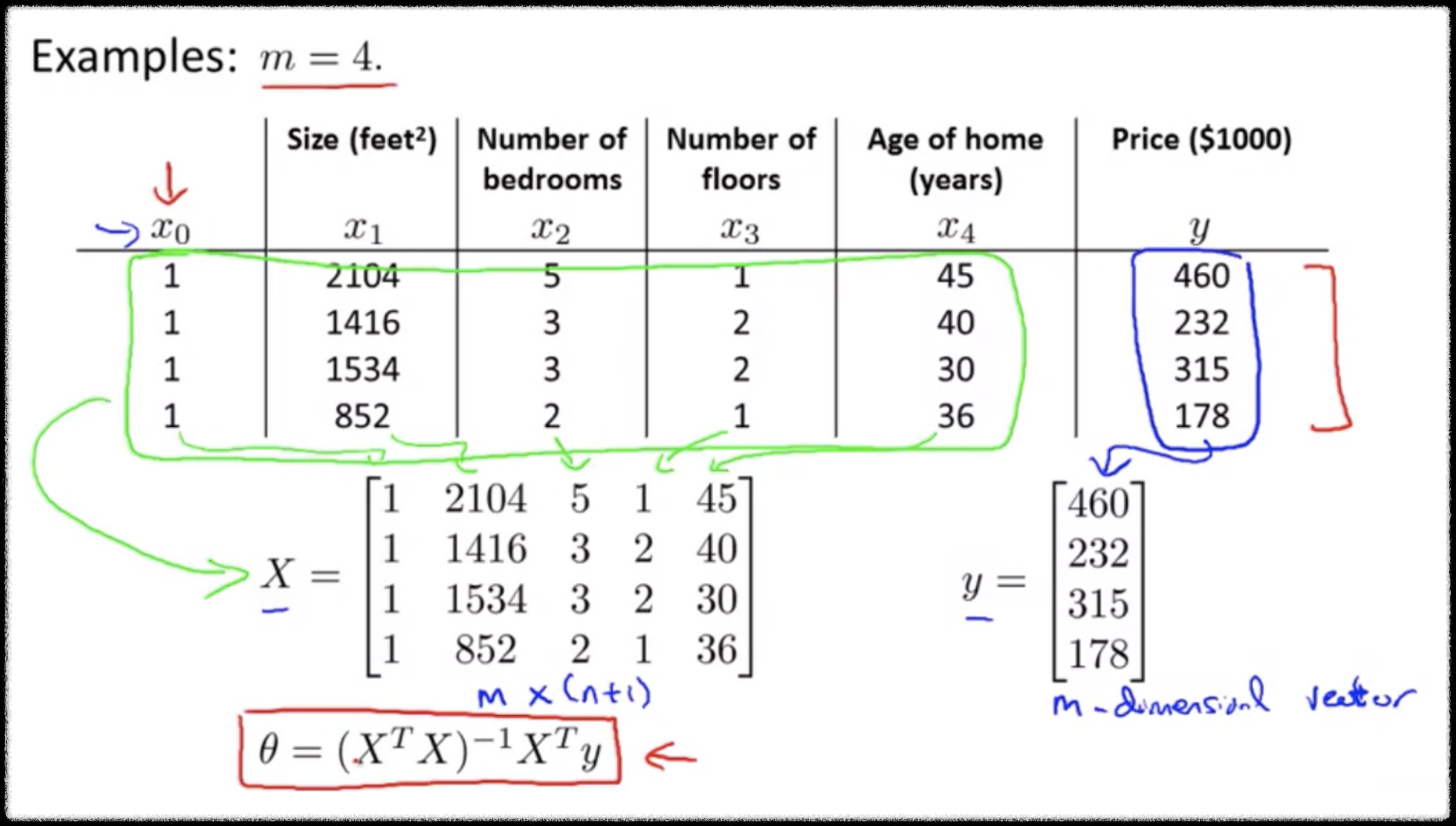
데이터셋에 x0 피쳐를 하나 추가하고 값은 항상 1이다.
행렬 X는 m X n+1차원의 행렬이다.
y는 m차원의 벡터다.
m은 학습 데이터의 숫자, n은 feature의 숫자이다.
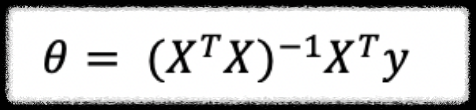
위의 식은 행렬 X와 벡터 y를 이용해서 파라미터 벡터를 구하는 공식이다.
출처: https://brunch.co.kr/@linecard/465
앤드류 응의 머신러닝 (4-6) : 정규 방정식
온라인 강의 플랫폼 코세라의 창립자인 앤드류 응 (Andrew Ng) 교수는 인공지능 업계의 거장입니다. 그가 스탠퍼드 대학에서 머신 러닝 입문자에게 한 강의를 그대로 코세라 온라인 강의 (Coursera.org
brunch.co.kr
import matplotlib.pyplot as plt
import numpy as np
x = 2 * np.random.rand(100,1) # [0, 1) 범위에서 균일한 분포 100 X 1 array
y = 4 + 3*x + np.random.randn(100,1) # normal distribution(mu=0,var=1)분포 100 X 1 array
plt.scatter(x,y)
plt.show()
x_b = np.c_[np.ones((100,1)),x] # 모든 샘플에 index 0번에 1을 추가
# np.linalg.inv는 넘파이 선형대수 모듈(linalg)의 inv(역함수)
# .dot은 행렬 곱셈
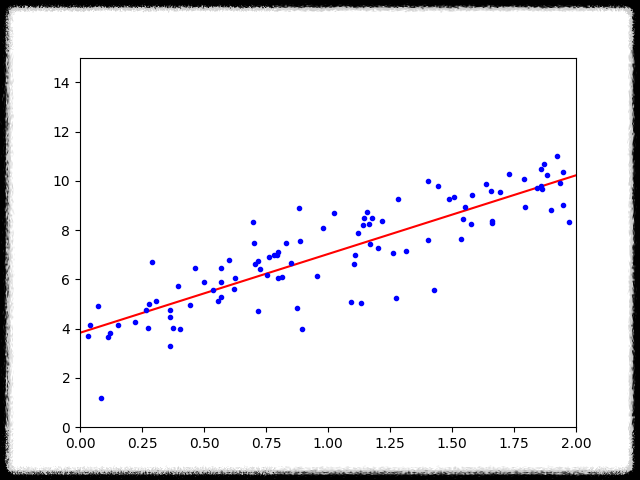
theta_best = np.linalg.inv(x_b.T.dot(x_b)).dot(x_b.T).dot(y)
print(theta_best)
# theta_best를 사용해서 y 값 예측
x_new = np.array([[0],[2]])
x_new_b = np.c_[np.ones((2,1)),x_new]
prediction = x_new_b.dot(theta_best)
print(prediction)
plt.plot(x_new,prediction,"r-")
plt.plot(x,y,"b.")
plt.axis([0,2,0,15]) # x축 범위 0~2, y축 범위 0~15
plt.show()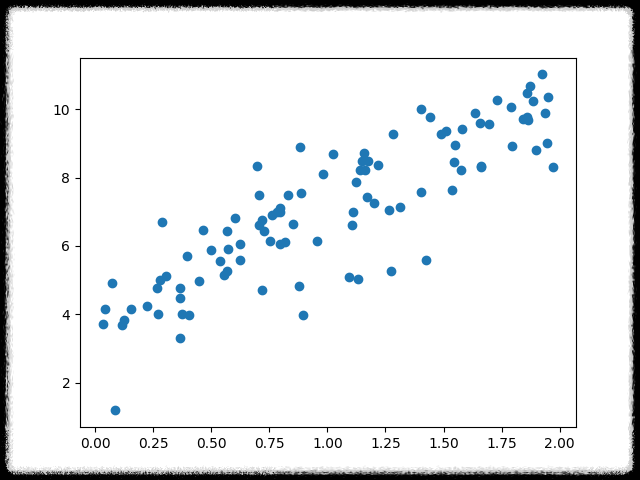
#사이킷런 라이브러리에서 제공하는 선형회귀 기능 위와 동일한 기능함.
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(x,y)
print(lin_reg.intercept_,lin_reg.coef_)
출처: https://velog.io/@changhtun1/python-선형-회귀-이론-및-실습
[Python] 선형 회귀 이론 및 실습
하나 이상의 특성과 연속적인 타깃 변수 사이의 관계를 모델링 하는 선형 회귀에 대해 파헤쳐보자!
velog.io
'AI & Data Science > LG Aimers' 카테고리의 다른 글
| 3. 지도학습(회귀,분류) - 3. Optimization(최적화) GD,Adam (0) | 2023.01.14 |
|---|---|
| 3. 지도학습(회귀,분류) - 2. Hypothesis, Cost Function (0) | 2023.01.14 |
| 3. 지도학습(회귀,분류) - 1. linear Regression, Bias, Variance, Drop out (1) | 2023.01.14 |
| LG Aimers 선정 & 수료 (0) | 2022.12.26 |



