Robot의 Motion Planning의 가장 큰 목표는 다음과 같다.
항상 최적의 path를 찾아야 하고, 최적의 path란 최단경로와 최소비용을 만족하는 것이다.
BFS)
너비 우선 탐색(Queue(FIFO)), 최단거리 보장
DFS)
깊이 우선 탐색(Stack(LIFO), 재귀), 최단거리 보장 x
DFS와 BFS는 올해 초에 블로그에 정리한 적이 있다.
https://geek-inside.tistory.com/entry/DFS
DFS & BFS
DFS와 BFS를 공부하기 앞서 큐와 스택에 대해서 간단하게 정리해봤다. 아래는 DFS에 관한 정리 및 구현 코드 이다. 재귀함수를 사용하는 것이 특징이다. 코드와 정리한 그림을 연결지어 생각하면
geek-inside.tistory.com
A* 알고리즘)
f(x) = g(x) + h(x)이다.
g(x)는 현재 상태 비용이다.
A* 알고리즘은 우선순위 큐를 사용한다.
h(x)는 휴리스틱 함수이다. 휴리스틱이란 경험적이라는 뜻을 갖고 있는데 즉 "이 정도 하면 대충 이 정도로 맞더라"라는 느낌으로 경험적으로 쓰는 것이다.
h(x)는 내가 공부하고 있는 시험 범위에서는 Manhatan Distance를 쓰는 것 같다.
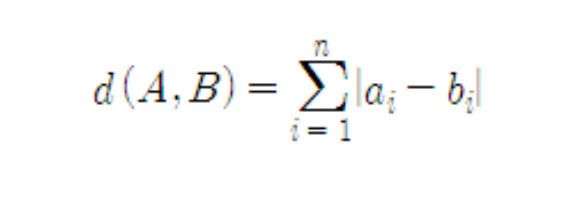
맨해튼 거리(Manhattan Distance)는 각 좌표의 차를 모두 더한 것을 거리로 한다.
|x1−x2|+|y1−y2| 가 두 점 사이의 맨해튼 거리이다.
0과 1로 이루어진 컴퓨터에서 맨해튼 거리는 사실상 최단경로와 의미가 같다.
만약 h(x)가 0일 경우 f(x)는 다익스트라 함수와 같다.
DP(플로이드-워셜 알고리즘))
이것도 내가 알고리즘 공부하면서 정리해봤다.
https://geek-inside.tistory.com/entry/플로이드-와샬Floyd-Warshall-알고리즘
플로이드 워셜(Floyd Warshall) 알고리즘
로봇공학을 공부하다가 알고리즘 파트가 나와서 공부해볼 겸 정리를 해본다. pdf에는 단순히 DP를 이용한 최단거리 탐색 이라고 적혀 있지만, 사실상 플로이드 워셜 알고리즘을 설명하고 있다.
geek-inside.tistory.com
Path Smoothing 알고리즘)
"""path_smoothing.ipynb
Automatically generated by Colaboratory.
Original file is located at
https://colab.research.google.com/drive/1pfUhNehKATJ0qScLdfrLIoLa5_nqD2ZG
"""
#기존 경로 = 입력경로
path = [[0, 0],
[0, 1],
[0, 2],
[1, 2],
[2, 2],
[3, 2],
[4, 2],
[4, 3],
[4, 4]]
path[1][0]
xx = [] #좌표 모음
yy = [] #y좌표 모음
for i,k in enumerate(path):
xx.append(k[0])
yy.append(k[1])
print(i,xx)
print(i,yy)
import matplotlib.pyplot as plt
plt.figure(figsize = (8,8))
plt.plot(xx,yy, "bo--")
# Make a deep copy of path into newpath
#newpath
newpath = [[0 for col in range(len(path[0]))] for row in range(len(path))]
for i in range(len(path)):
for j in range(len(path[0])):
newpath[i][j] = path[i][j]
weight_data = 0.5
weight_smooth = 0.1
tolerance = 0.00001
for i in range(1,len(path)-1):
for j in range(len(path[0])):
newpath[i][j] = newpath[i][j] + weight_data*(path[i][j]-newpath[i][j]) #공식1
newpath[i][j] = newpath[i][j] + weight_smooth*(newpath[i+1][j]+newpath[i-1][j]-2*newpath[i][j]) #공식2
print(newpath[i][j])
newpath
for i in range(len(path)):
print ('['+ ', '.join('%.3f'%x for x in path[i]) +'] -> ['+ ', '.join('%.3f'%x for x in newpath[i]) +']')
xx2 = []
yy2 = []
for i,k in enumerate(newpath):
xx2.append(k[0])
yy2.append(k[1])
plt.figure(figsize = (8,8))
plt.plot(xx,yy, "bo--")
plt.plot(xx2,yy2, "ro--")
def smooth(path, weight_data = 0.5, weight_smooth = 0.1):
newpath = [[0 for col in range(len(path[0]))] for row in range(len(path))]
for i in range(len(path)):
for j in range(len(path[0])):
newpath[i][j] = path[i][j]
for i in range(1,len(path)-1):
for j in range(len(path[0])):
newpath[i][j] = newpath[i][j] + weight_data*(path[i][j]-newpath[i][j])
newpath[i][j] = newpath[i][j] + weight_smooth*(newpath[i+1][j]+newpath[i-1][j]-2*newpath[i][j])
return newpath
newpath2 = smooth(path,0.6,0.1)
xx3 = []
yy3 = []
for i,k in enumerate(newpath2):
xx3.append(k[0])
yy3.append(k[1])
plt.figure(figsize = (8,8))
plt.plot(xx,yy, "bo--")
plt.plot(xx2,yy2, "ro--")
plt.plot(xx3,yy3, "go--")
newpath3 = smooth(path,0.8,0.2)
xx4 = []
yy4 = []
for i,k in enumerate(newpath3):
xx4.append(k[0])
yy4.append(k[1])
plt.figure(figsize = (8,8))
plt.plot(xx,yy, "bo--")
plt.plot(xx2,yy2, "ro--")
plt.plot(xx3,yy3, "go--")
plt.plot(xx4,yy4, "m*--")위의 코드를 보면 핵심적인 식은 다음과 같다.
newpath[i][j] = newpath[i][j] + weight_data*(path[i][j]-newpath[i][j])
newpath[i][j] = newpath[i][j] + weight_smooth*(newpath[i+1][j]+newpath[i-1][j]-2*newpath[i][j])새로운 경로인 newpath, 는 (초기 path - newpath)*weight_data + newpath이다.
이렇게 새롭게 설정된 newpath는 다시 자기 자신의 위와 아래에 있는 좌표의 합과 자신을 두배 곱한 것의 차에 weight_smooth를 곱한 뒤 newpath에 더해진다. 이를 반복하면 경로가 유연해진다.(평활화된다.)
PID)
PID란 목표값과의 오차를 빠르게 줄여서 빠른시간에 목표값에 도달할 수 있도록 하는 제어기의 일종이다.
P = kp*e(t)
I = ki Integral(t to 0 e(t) dt )
D = kd * d/dt * e
'Computer Science > 기타' 카테고리의 다른 글
| (주)「윈스」 인턴십 합격 후기 & 코딩테스트 후기 (3) | 2022.12.15 |
|---|---|
| 기술 면접 질문 모음 (0) | 2022.12.10 |
| 로봇공학 정리 - 1(베이즈 정리, 베이즈 필터, Particle 필터) (0) | 2022.11.03 |
| 네이버 부스트캠프 AI Tech 4기 1차 코딩테스트 후기 (0) | 2022.08.12 |
| 오픈소스 기말고사 정리 (0) | 2022.06.12 |


